Why Bother with Theory? The One Concept Engineers Can’t Ignore
Let’s be honest, as engineers, we’re trained to solve problems. We want to get our hands dirty in the software, set up the simulation, and get results. The deep, dense theory can feel like a roadblock. But when it comes to the Navier-Stokes equations, ignoring the basics is like a pilot ignoring how wings generate lift. You might be able to press the buttons, but you won’t understand why the plane is flying—or why it just crashed.
Understanding the physical meaning behind these equations is the difference between blindly trusting a colorful plot and confidently making a multi-million dollar design decision. It’s what separates a technician from an expert. At its core, it’s all part of the bigger picture of What CFD is all about, turning complex physics into practical engineering solutions. This isn’t just academic gatekeeping; it’s about preventing costly errors before they happen.
Deconstructing the Beast: The Navier-Stokes Equations in Plain English
Think of the Navier-Stokes equations as the ultimate recipe for fluid motion. They don’t look friendly, I get it. But forget the scary Greek letters for a minute. The whole thing is just a fancy way of stating Newton’s second law (F=ma) for a tiny parcel of fluid. It’s a statement about momentum conservation.
We’re just going to look at the main “ingredients” in this recipe, one by one, to see what they actually do in the real world and inside your CFD software.
The Inertia Term: Where is the fluid going? (Convection)
This is the part that describes how a fluid parcel carries its own momentum around. Picture a fast-moving river. A floating leaf isn’t just pushed by the water around it; it’s carried along by the bulk motion of the flow. That’s convection. In CFD, this term is responsible for the direction and magnitude of your velocity vectors. When you see those beautiful streamlines swooping over an airfoil, you’re looking at inertia in action.

The Pressure Term: The “push” that drives the flow
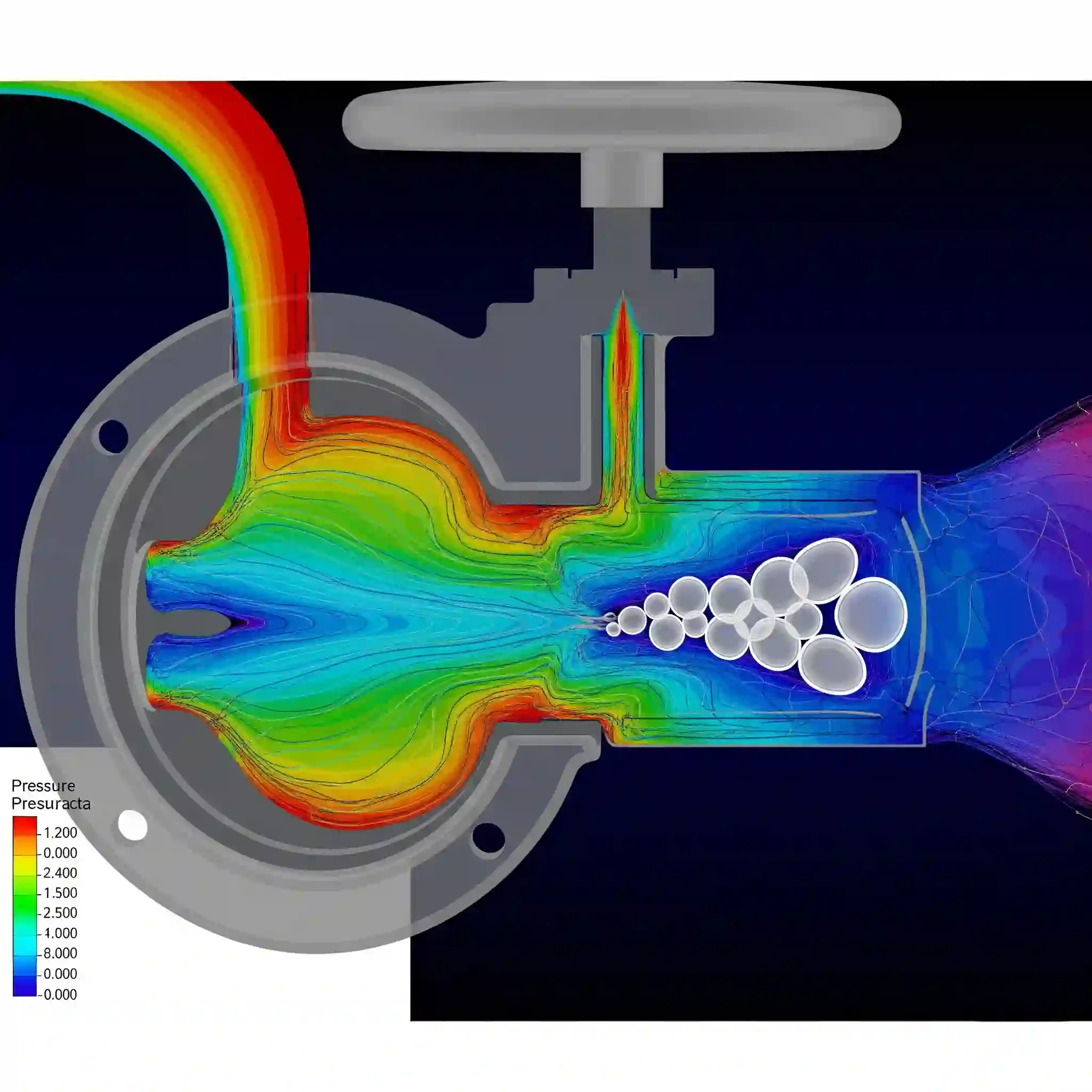
Fluid doesn’t move on its own. It needs a push. This term is that push. Specifically, it’s about the pressure gradient—the difference in pressure from one point to another. Fluid always wants to move from high pressure to low pressure, just like air rushing out of a punctured tire. This is arguably the most important term for engineers, as it’s directly responsible for calculating crucial forces like aerodynamic lift and drag, or the pressure drop across a valve. Understanding this helps you interpret many of the real-world CFD applications like F1 cars.
The Viscous Term: The “friction” inside the fluid
Ever tried to pour honey and water? That difference in “thickness” or resistance to flow is viscosity. This term represents the internal friction within the fluid. It’s what creates the “no-slip” condition, the fundamental rule that fluid sticks to a surface it’s in contact with. This, in turn, creates the boundary layer, a thin region near a surface where the velocity changes dramatically.
I learned this the hard way about 15 years ago on a project for a pump manufacturer. My early simulations showed a much higher impeller efficiency than their physical tests. For weeks, I checked my setup. The problem? My mesh was too coarse near the blade surfaces to properly capture the viscous effects in the boundary layer. The simulation was essentially seeing a frictionless, “slippery” blade. It was a humbling reminder that understanding The Navier-Stokes Equations for Engineers isn’t just academic; every term matters. A better mesh that captured the viscous losses gave us results within 2% of the experiment.
The External Forces Term: How gravity or other forces play a role
This is usually the most straightforward part of the recipe. It’s the “catch-all” for any body forces acting on the entire fluid. The most common one is gravity 👇. If you’re simulating water sloshing in a tank or natural convection where hot air rises, you absolutely need to include this term. For other advanced applications, this could also be an electromagnetic force or the Coriolis force for large-scale geophysical flows.
“Solving” Navier-Stokes: Why Your Laptop Can’t Do It (And Why We Need CFD)
Here’s the kicker. Except for a few very simple, idealized cases, there is no exact, pen-and-paper solution to these equations. They are notoriously difficult to solve analyticaly. This is not an exaggeration; it’s one of the biggest unsolved problems in mathematics.
So, what do we do? We cheat. Or rather, we approximate. This is where Computational Fluid Dynamics comes in. Software like ANSYS Fluent, OpenFOAM, or Simcenter STAR-CCM+ doesn’t find the exact solution. Instead, it breaks your geometry into millions of tiny cells (a mesh) and solves a simplified version of the equations for each cell, iterating until the solution converges. This entire workflow, from meshing to getting results, is what our CFD analysis services are designed to handle, navigating the complexities to deliver reliable engineering data. The sheer number of calculations is why you need powerful computers—and often, specialized expertise.
The CFDSource Approach: How We Turn Complex Math into Actionable Engineering Insights
So if we can’t solve the equations perfectly, how do we get trustworthy results? This is the core of what we do. It’s not magic; it’s a disciplined engineering process. We translate the continuous, infinitely complex world of fluid dynamics into a language a computer can understand.
From Continuous Equations to a Finite Grid: The Magic of Discretization
First, we perform “discretization.” Imagine trying to describe a perfect circle using only tiny, straight lines. If you use enough lines, your shape will be almost indistinguishable from the real circle. That’s what we do to the Navier-Stokes equations. We convert the smooth, continuous calculus into a system of algebraic equations that can be solved for a finite number of points in space and time. This whole process is a crucial part of the core stages of any CFD simulation, starting right after you import your CAD model.
Meshing is Not Just Art, It’s Physics: How the Right Mesh Captures the Right Physics
Those “finite number of points” live on a mesh. A mesh is the 3D grid of cells we create inside our geometry. This step is critical and, honestly, where many projects go wrong. A good mesh needs to be fine enough in important areas (like near surfaces, in small gaps) to capture the physics, but not so fine everywhere that the simulation takes weeks to run. It’s a constant trade-off between accuracy and compuational cost. Getting it right requires experience, not just clicking “generate mesh.” 🧐
Practical Implications in Your CFD Software (ANSYS Fluent, OpenFOAM, etc.)
When you open your CFD software, you’re not typing in the Navier-Stokes equations. Instead, you’re making choices that tell the software how to simplify and solve them for your specific problem. Here are two of the biggest decisions you’ll make.
Laminar vs. Turbulent: Which Assumption Simplifies the Equations for Your Problem?
Is your flow smooth and predictable like honey pouring from a jar (laminar), or chaotic and messy like a raging river (turbulent)? This is the first question you must answer. If you choose “laminar,” the software solves the equations as we’ve discussed. But most industrial flows are turbulent. For those, we can’t possibly simulate every tiny swirl and eddy. Instead, we use a “turbulence model” (like k-epsilon or k-ω SST), which adds extra equations to approximate the average effect of turbulence. Your choice here dramatically impacts the results.
Steady-State vs. Transient: Are You Capturing a Snapshot or a Movie of the Flow?
Does the flow behavior change over time, or is it basically constant? A steady-state simulation solves for the final, unchanging condition—like a single photograph of the flow field. A transient simulation solves step-by-step through time—like a movie. Simulating the constant flow of air over a car at cruising speed can be steady-state. Simulating a valve slamming shut or water sloshing in a tank must be transient. Transient simulations are much more computationally expensive, so you only use them when you have to.
A Common Failure Point We See at CFDSource: Misinterpreting Turbulence Models
One of the most frequent sources of error we see from clients who have tried to run simulations in-house is the blind application of a default turbulence model. The standard k-epsilon model is a fantastic workhorse, but it struggles with flows that separate from a surface (like airflow stalling on a wing). Using it in the wrong situation can lead to results that look plausible but are physically wrong. This is where knowing how accurate CFD can be, and what its limits are, is so vital. You need to understand the assumptions baked into the models you select.
The Bottom Line: What Navier-Stokes Tells You About Your Design
At the end of the day, we grapple with all this complexity for one reason: to get actionable data that improves a design. By solving these equations, we can predict things that are difficult, expensive, or sometimes impossible to measure physically.
Here’s what you actually get:
- Velocity Fields: Find dead zones in a mixing tank or high-velocity areas causing erosion.
- Pressure Maps: Calculate the lift on a wing or the drag on a vehicle.
- Heat Transfer Rates: Ensure a CPU cooler is effective or predict thermal stress in an engine.
- Flow Paths: Track pollutants from a smokestack or ensure even flow distribution in a manifold.
This data allows you to compare different designs digitally, which is often much faster and cheaper than the alternative of building and testing physical prototypes.
Ready to Harness the Power of Fluid Dynamics for Your Project?
The journey from a complex partial differential equation to a tangible design improvement is what makes this field so powerful. These equations aren’t just academic exercises; they are the fundamental tool we use to understand and predict the physical world. For many projects, running your own analysis is a great way to learn. For complex, high-stakes industrial problems where accuracy is non-negotiable, partnering with experienced CFD analysis companies can de-risk your project and accelerate your time-to-market. Ultimately, a practical understanding of the Navier-Stokes equations for engineers empowers you to ask the right questions and make smarter decisions, whether you’re running the simulation yourself or interpreting the results from an expert.


