CFD analysis: Computational Fluid Dynamics (CFD) is a powerful tool used in engineering and scientific research for simulating and analyzing fluid flow and heat transfer. This essay explores the principles and applications of CFD analysis, focusing on the role of CFD simulation and modeling in understanding complex fluid dynamic phenomena.

Introduction
Computational Fluid Dynamics (CFD) is a multidisciplinary field that has transformed the way engineers and scientists approach fluid flow problems. It is a numerical simulation technique that allows the detailed analysis of fluid behavior in a wide range of scenarios, from the flow of air over an aircraft wing to the complex dynamics of blood circulation in the human body. The term “computational” emphasizes the central role of computers in CFD, where complex mathematical equations governing fluid motion are solved using numerical methods.
CFD has become an indispensable tool in research and engineering, providing insights into fluid dynamics that were once impossible to obtain experimentally. With its ability to simulate, visualize, and analyze fluid behavior, CFD has applications in a multitude of industries, from aerospace to biomedicine, and is continuously advancing as computing power and modeling techniques improve.
Historical Overview of CFD
To appreciate the significance of Computational Fluid Dynamics (CFD), it is essential to delve into its historical roots. The foundations of CFD can be traced back to the early 20th century when engineers and scientists began formulating mathematical models to describe fluid flow. However, the computational aspect of CFD only gained prominence in the mid-20th century with the advent of digital computers. One of the pivotal moments in CFD history was the development of the Navier-Stokes equations, a set of partial differential equations that describe the fundamental principles of fluid motion.
These equations serve as the backbone of CFD, allowing the simulation of a wide range of fluid dynamic scenarios. Over the years, advancements in numerical techniques and computing power have propelled CFD to the forefront of engineering and scientific research, enabling the analysis of complex fluid phenomena that were previously beyond our reach.
Governing Equations in CFD
At the core of Computational Fluid Dynamics (CFD) lie the fundamental governing equations that describe the behavior of fluids. The Navier-Stokes equations are the primary set of equations that underpin CFD simulations. These equations, named after Claude-Louis Navier and George Gabriel Stokes, capture the principles of fluid dynamics, including the conservation of mass, momentum, and energy. The continuity equation ensures that mass is conserved within a fluid domain, while the momentum equations govern the fluid’s velocity and pressure distributions.
The energy equation accounts for heat transfer and temperature variations within the fluid. Solving these equations numerically is the essence of CFD modeling. Depending on the specific application, additional physics, such as turbulence, combustion, and multiphase flow, may be incorporated into the model. The accuracy and reliability of CFD simulations heavily rely on the fidelity with which these governing equations are solved, making them a focal point of research and development in the field.

CFD Modeling: An Overview
CFD modeling is a crucial aspect of CFD analysis, as it involves the formulation of numerical methods and models to represent fluid behavior in a computationally feasible manner. There are various types of CFD models, each suited to different flow conditions and scales. Reynolds-Averaged Navier-Stokes (RANS) models are widely used for industrial applications, offering a compromise between accuracy and computational efficiency. For turbulent flows, Large Eddy Simulation (LES) and Direct Numerical Simulation (DNS) models provide more detailed insights, but at a significantly higher computational cost.
The choice of model depends on the specific problem at hand. CFD modeling also entails selecting appropriate boundary conditions and initial conditions, which define how the fluid interacts with its surroundings and its initial state. This step is crucial for accurately representing real-world scenarios in simulations. Moreover, the numerical method used, such as Finite Difference, Finite Volume, or Finite Element, plays a significant role in the accuracy of CFD simulations. Meshing techniques, including grid generation and quality, are vital in ensuring that the numerical solution converges to a physically meaningful result. Overall, CFD modeling is a complex and multifaceted process that requires a deep understanding of both fluid dynamics and numerical methods to produce meaningful and reliable results.
Numerical Methods in CFD
In the realm of Computational Fluid Dynamics (CFD), numerical methods are the essential tools that enable the transformation of complex fluid dynamics equations into computationally tractable problems. There are several numerical methods employed in CFD, each with its strengths and applications. The Finite Difference Method (FDM) discretizes the governing equations by approximating derivatives using finite differences. While conceptually straightforward, FDM is mainly used for simple geometries and structured grids due to its simplicity. The Finite Volume Method (FVM) is one of the most commonly used techniques in CFD.
It divides the domain into control volumes, allowing for a conservative approach to mass, momentum, and energy conservation. This method is highly adaptable and works well with complex geometries. The Finite Element Method (FEM), often associated with structural analysis, is also applied to CFD. It discretizes the domain into finite elements, allowing for great flexibility in handling irregular geometries and varying grid resolutions. Each of these methods has its strengths and weaknesses, and the choice depends on the specific problem being addressed. These numerical methods lay the groundwork for CFD simulations, forming the basis for the translation of physical fluid dynamics into mathematical models that computers can solve.

Meshing Techniques in CFD Simulation
Meshing is a critical component of Computational Fluid Dynamics (CFD) simulation, as it directly impacts the accuracy and computational efficiency of the results. Meshing involves dividing the computational domain into discrete elements, or cells, that allow the numerical methods to be applied. There are two primary types of meshing: structured and unstructured. Structured meshing arranges grid cells in an organized manner, typically using a Cartesian or curvilinear grid. This approach is well-suited for simple geometries and can lead to better numerical stability. However, it is often less flexible when dealing with complex or irregular shapes. Unstructured meshing, on the other hand, provides greater flexibility.
It allows for the generation of grids that conform closely to the geometry being simulated. This is particularly valuable for problems with intricate geometries, such as aerospace components or biological systems. The quality of the mesh is also of paramount importance; irregularities or poorly constructed grids can introduce errors into the simulation. Grid refinement, which increases mesh resolution in areas of interest, is a technique commonly employed to enhance accuracy. Proper meshing techniques and grid quality are pivotal to achieving reliable CFD results, and considerable research is dedicated to improving mesh generation processes.
Boundary Conditions in CFD
Boundary conditions are a fundamental aspect of Computational Fluid Dynamics (CFD) simulations, as they define how the fluid interacts with its surroundings and establish the initial state of the flow field. Prescribing appropriate boundary conditions is essential for simulating realistic scenarios. There are several types of boundary conditions in CFD. The most common ones include inlet conditions, where the fluid properties (velocity, temperature, etc.) entering the domain are specified, and outlet conditions, which describe the flow properties as the fluid exits the computational domain.
Wall conditions are crucial for representing the interaction of fluids with solid surfaces. Various wall models, such as no-slip conditions for viscous flows, are used to ensure fluid adheres to walls as expected. Moreover, symmetry and periodic boundary conditions can be applied to save computational resources when simulating repetitive or symmetrical geometries. The choice of boundary conditions is highly problem-specific and plays a significant role in the accuracy and reliability of CFD simulations. Appropriate boundary conditions ensure that the numerical model accurately reflects the real-world behavior of the fluid.
CFD Simulation Process
The CFD simulation process involves several key stages, from pre-processing to post-processing, each contributing to the successful execution of a numerical experiment. Pre-processing is where the problem setup occurs. This stage involves defining the geometry to be simulated and creating the grid (mesh) that will cover the domain. Boundary conditions and initial conditions are established, ensuring that the simulation accurately reflects real-world conditions. Once the problem is set up, the simulation stage begins, where the numerical solution of the governing equations takes place. This is often the most computationally intensive part of the process, and it relies on powerful computers and parallel computing techniques to accelerate the calculations. Various CFD software packages provide tools to facilitate the simulation stage.

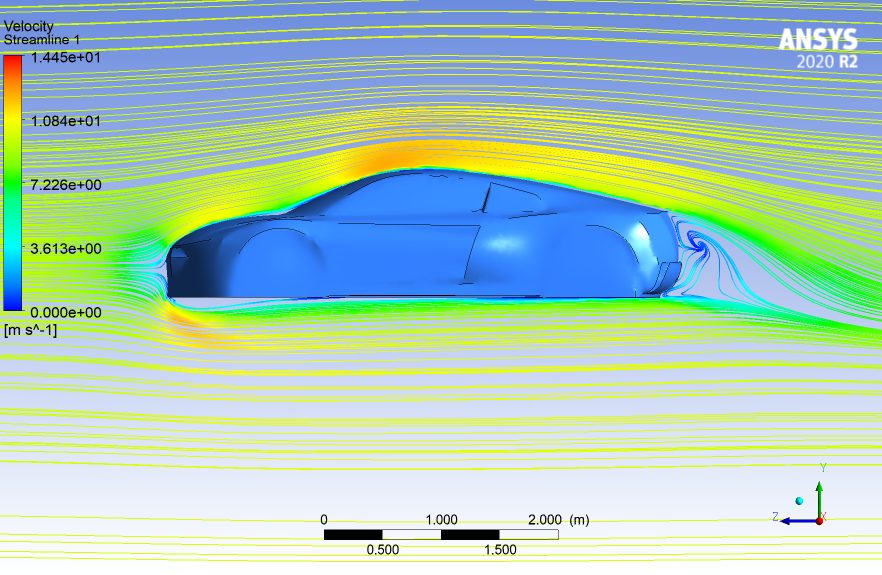
Post-processing, the final stage, involves the analysis and visualization of simulation results. Engineers and scientists use this stage to interpret the data generated during the simulation. Visualization techniques, such as flow field contours, vector plots, and streamlines, help in understanding the fluid behavior. Quantitative data, such as pressure distributions and heat transfer coefficients, are extracted for analysis and design optimization.
The post-processing phase also enables the comparison of simulation results with experimental data, allowing for validation and verification of the CFD model. The iterative nature of the CFD simulation process often means revisiting the pre-processing stage to fine-tune the model or grid for improved results. Understanding the intricacies of each stage and how they interconnect is essential for successful CFD simulations that provide valuable insights into fluid dynamics.
Turbulence Modeling in CFD
Turbulence is a ubiquitous and challenging aspect of fluid flow that plays a significant role in many real-world applications. In Computational Fluid Dynamics (CFD), turbulence modeling is a crucial component of accurately simulating complex turbulent flows. Turbulence is characterized by chaotic, unsteady fluid motion with a wide range of scales. To model turbulence in CFD, various approaches are employed. The Reynolds-Averaged Navier-Stokes (RANS) models are commonly used for industrial applications. These models assume that the flow properties can be decomposed into time-averaged and fluctuating components, simplifying the governing equations.
The k-ε and k-ω models are among the most popular RANS models, providing reasonable accuracy for a wide range of turbulent flows. For more detailed simulations, especially in situations with significant vortical structures, Large Eddy Simulation (LES) and Direct Numerical Simulation (DNS) models are employed. LES resolves larger turbulent structures while modeling smaller ones, making it suitable for high-Reynolds-number flows. DNS, on the other hand, directly resolves all turbulent scales, offering the most accurate representation but at an exceptionally high computational cost. The choice of turbulence model depends on the specific application and available computational resources, highlighting the importance of selecting the right modeling approach to ensure accurate CFD simulations.
Validation and Verification of CFD Models
Ensuring the accuracy and reliability of Computational Fluid Dynamics (CFD) models is a paramount concern in the field. To this end, validation and verification processes are essential to confirm that the CFD simulations align with reality and are free from errors. Verification primarily involves examining the numerical aspects of the simulation, including the accuracy of the numerical methods, grid resolution, and consistency of the results. Verification ensures that the CFD code and its implementation are working correctly.
Validation, on the other hand, focuses on comparing CFD results to experimental data or analytical solutions to confirm that the model accurately represents the physical behavior of the fluid. Achieving validation involves a meticulous process of conducting experiments, generating suitable data for comparison, and assessing the agreement between the simulated and observed data. It’s important to note that verification is a necessary, but not sufficient, condition for validation. Validation often requires access to experimental facilities or data, making it a resource-intensive process. Despite these challenges, validation and verification are indispensable for building trust in CFD models, enabling engineers and scientists to make informed decisions based on CFD results with confidence.
Conclusion
In conclusion, Computational Fluid Dynamics (CFD) stands as a transformative force in the world of engineering, science, and beyond. The journey through the intricacies of CFD has provided insights into the foundational principles, numerical methods, and diverse applications that make this discipline indispensable. CFD, rooted in historical developments and driven by the power of high-performance computing, has become a cornerstone of problem-solving and innovation.
Its impact resonates across industries, including aerospace, automotive engineering, environmental studies, and the oil and gas sector, as well as the vital realms of biomedicine and civil engineering. CFD has extended its influence into critical areas, addressing global concerns such as environmental sustainability, pollution control, and public health. The future holds both challenges and promises, as CFD endeavors to tackle intricate geometries, embrace Multiphysics, and advance turbulence modeling. Open-source CFD software, fostering a global community of collaboration, further democratizes access to this potent tool.
As we look ahead, the future of CFD is marked by endless possibilities. It promises to expand its role, entering new domains and confronting uncharted territories. Whether it involves the quest for cleaner energy, the development of groundbreaking medical technologies, or the design of resilient and sustainable urban landscapes, CFD remains a guiding light, illuminating our path to a more informed, efficient, and responsible world. Its journey is far from over, and the ongoing advancements in CFD offer a future where the complexities of fluid dynamics yield to our ever-growing capacity to model, simulate, and understand the intricacies of the fluid world that surrounds us.
CFD analysis, Modeling & Simulation: CFD represents the convergence of science, engineering, and innovation, pushing the boundaries of what we can achieve and how we can comprehend the fluid dynamics that shape our lives and the world around us. It is a journey marked by progress, challenges, and triumphs, and its continued evolution is set to leave an indelible mark on the way we approach and solve complex fluid dynamics problems in a world where these challenges have never been more critical or exciting.